Confusing P-values with Clinical Impact: The Significance Fallacy
Disclaimer: This post is largely not an argument for or against the recent remdesivir findings. Rather, it’s meant to help you better distinguish the importance of clinical findings from the quality of the evidence for or against those findings. These two often get conflated in the news—even by medical doctors and health experts!
Technical Disclaimer: We’ll analyze time to recovery as a continuous variable for simplicity, though a time-to-event / survival analysis is more appropriate.
Main Lessons
- Ask yourself if an RCT’s reported effect size estimate is meaningful, regardless of sample size.
- Train yourself to internalize that significance does not imply importance.
- Remember that sample size does not correlate with effect size.
- Never just say “significant” when you really mean “statistically significant”. You will be misunderstood as saying “important”. Instead, always say or write out the whole phrase “statistically significant”.
Introduction
Remdesivir made headlines again recently thanks to some new findings of its possible efficacy at reducing the time to recovery for hospitalized COVID-19 patients. Keep in mind this is only one randomized controlled trial (RCT), so we won’t really know much until more remdesivir RCTs are done. But we can learn much even from this one trial and how it’s being reported.
In reading or watching news on RCTs, look for these two things:
Significant Confusion. When you hear someone in the news write or talk about a “significant” finding from an RCT, assume that they want to tell you about whether or not it is clinically or scientifically meaningful or useful. But instead, they’ll report its statistical significance when they really wanted to report its scientific or clinical importance. They’ll tell you how good the evidence is when they really wanted to tell you how useful the treatment is. This is because they’re mistaking the scientific or clinical thing they want to tell you (i.e., importance) with the quality of the evidence for that thing (i.e., statistical significance)—without honestly realizing this is what they’re doing. This is called the “significance fallacy” (Kühberger et al, 2015; Silva-Ayçaguer et al, 2010; Barnett and Mathisen, 1997).
(Effect) Size Matters. Also listen to what they report as the estimated size of the effect (e.g., reduction in time-to-recovery from 15 days under placebo down to 11 days under remdesivir). That this finding is “statistically significant” only means there was enough statistical evidence in this particular study to say that the observed difference may be real (i.e., enough patients were enrolled to detect that average difference). Ask yourself, is that effect size meaningful or useful in actual medical, clinical, and hospital care? Is a 4-day reduction enough? Maybe, maybe not, depending on the situation and what’s needed in a given community or hospital. (See, for example, Sullivan and Feinn, 2012.)
Unfortunately for our reporter or health official, we’ll see below how statistical significance does not imply scientific or clinical importance. When reading or listening to such reports, never, never, never ever just latch onto the word “significant”. It usually means “statistically significant”, and is useless without the context of the effect size and its clinical usefulness.
But before you dismiss this as “pedantic statistical policing”, read on…
Two Hypothetical Scenarios
It is mathematically impossible to tell if a finding is clinically or scientifically important just from knowing whether or not it was “statistically significant”.
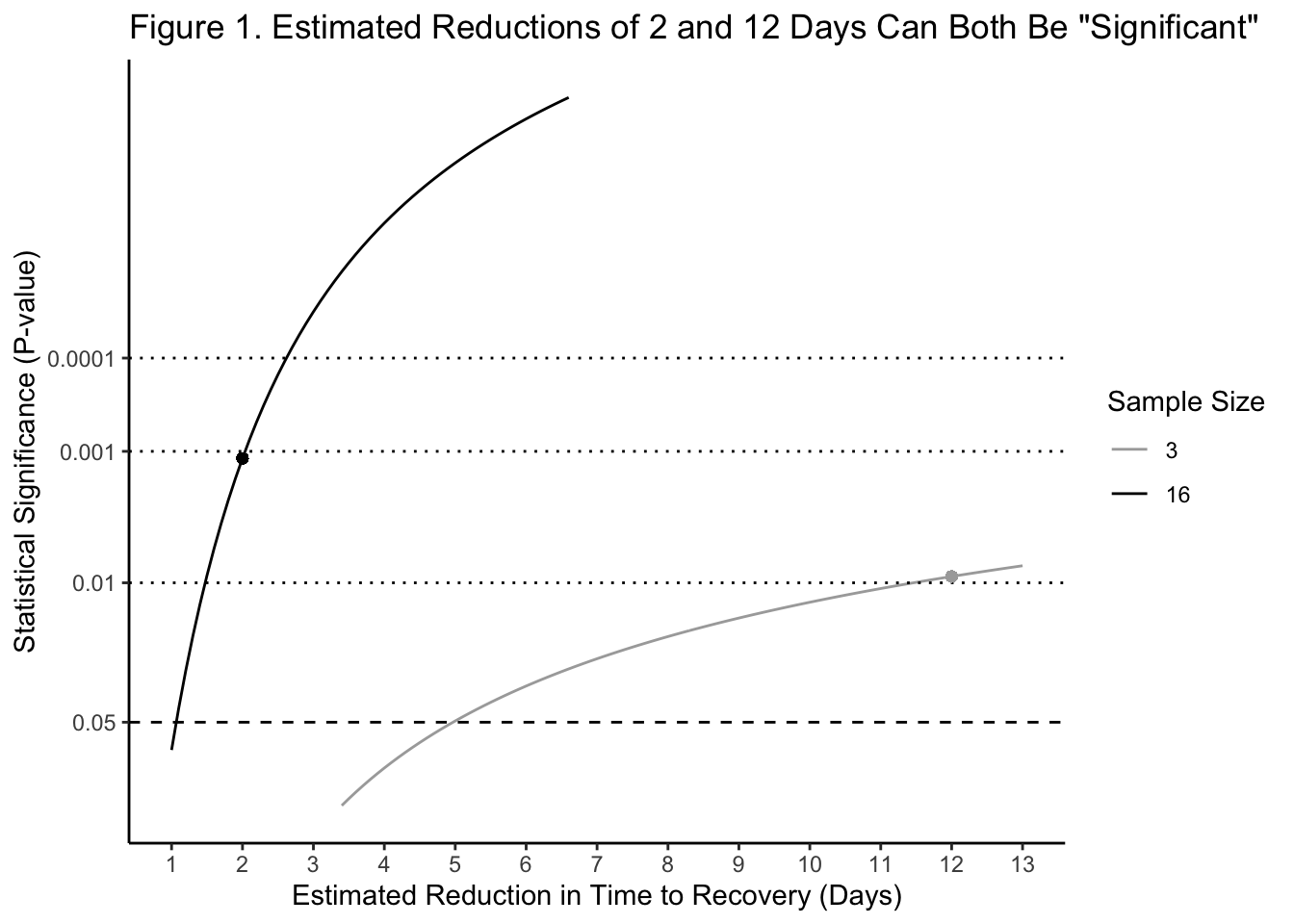
In an RCT, a “statistically significant” effect is one with enough statistical evidence in favor of the hypothesized effect versus either no effect or some other baseline effect (e.g., from a standard of care). Does this mean the finding is actually clinically or scientifically meaningful? Maybe, maybe not. It is mathematically impossible to tell if a finding is clinically or scientifically important just from knowing whether or not it was “statistically significant”. (See Figures 1 and 2 and the Appendix for an example and proof sketch.)
Even for a given effect size, statistical significance can only tell you how big your sample was—not how important that effect size is. And sample size does not correlate with effect size in general: Enrolling more patients can increase statistical significance, but it doesn’t improve or reduce the clinical impact of your drug. (It is what it is.)
That is, “statistical significance” has everything to do with the quality of evidence. But it has nothing to do with “clinical importance” (i.e., if what the evidence shows is meaningful or useful). The confusion arises because in an RCT, “statistical significance” is produced by either a really big treatment effect or lots of evidence for an effect. Most people—myself included—naturally think of the word “significant” to mean the former. However, a finding will still be “statistically significant” when only one of these things is true, as in the two hypothetical Scenarios below.
First, let’s assume the effects are identical for all patients, but that the time to recovery varies by 2 days on average (i.e., the standard deviation is 2 days). Let’s also assume 15 days is the true baseline time to recovery (i.e., control outcome), so we will design single-arm trials wherein all patients get remdesivir.
In Figure 1, we see that a big estimated reduction of 12 days to recovery from a hypothetical study enrolling 3 patients would qualitatively be just as “significant” (p = 0.0091) at the 0.05 statistical significance level as a small estimated reduction of 2 days (p = 0.0012) from a study enrolling 16 patients. But this makes no sense as a statement of clinical importance!
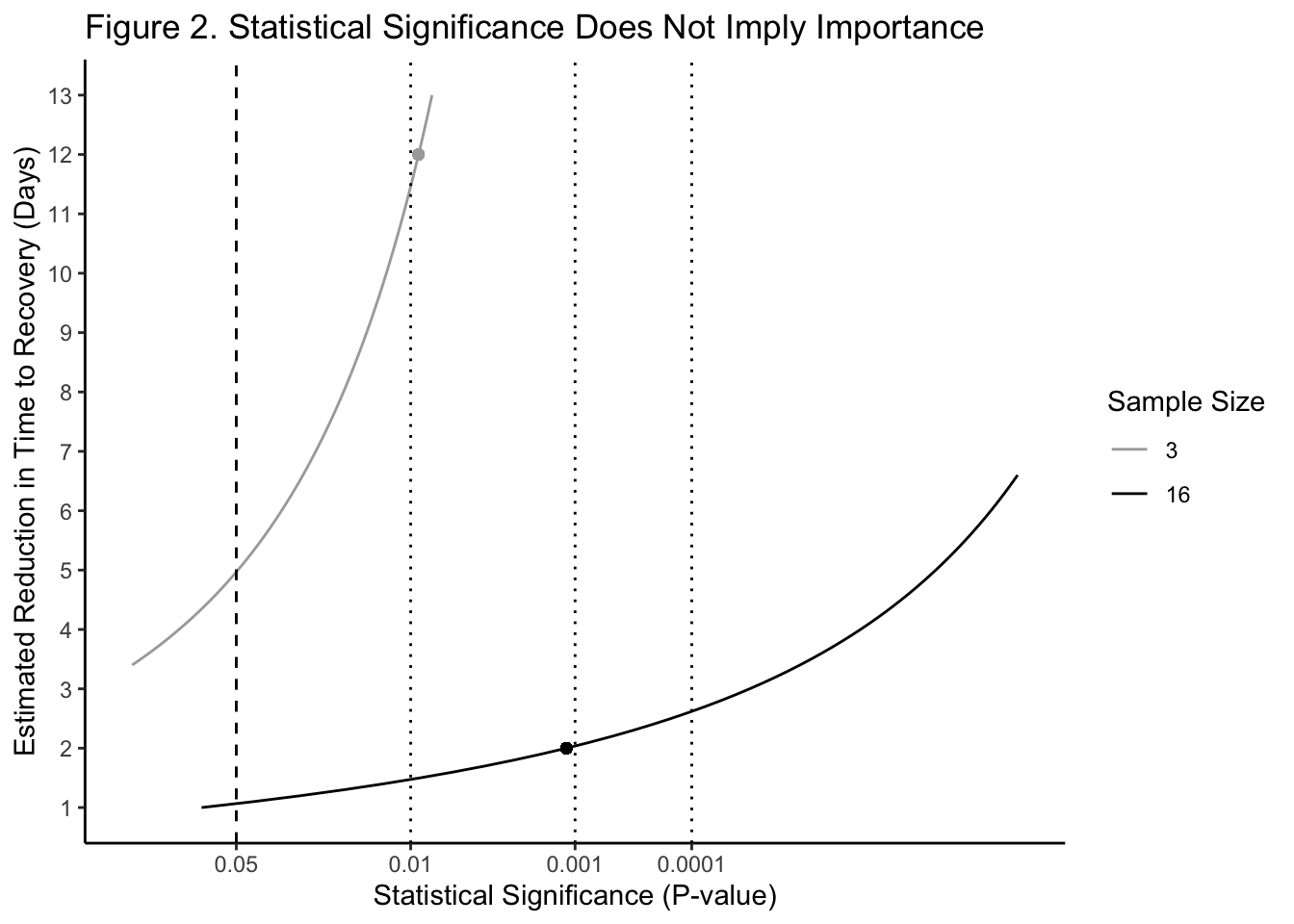
This might be clearer in Figure 2, with the axes flipped: An estimated average reduction of 12 days (y-axis) is less “significant” (x-axis; p = 0.0091) than one of 2 days (p = 0.0012). (Figures 1 and 2 were created using a two-sided t-test with standard deviation set to 2 days. See the Appendix for code and details.)
Sample size does not correlate with effect size.
To elaborate on these two Scenarios:
There’s a big true effect, but little evidence. Suppose remdesivir in fact greatly reduces time to recovery by 12 days on average. We enroll 3 patients in a follow-up single-arm RCT, and estimate this unknown true effect as an average reduction of 10.6 days—complete with a “significant p-value” at the 0.05 level of 0.0157. The effect is so big that we only needed 3 patients to see it. (Remember, one RCT only provides one estimate of the true effect. We will almost certainly estimate the true effect with some variation every time; here, 10.6 days as an estimate of the true average effect of 12 days. The p-value will also vary from sample to sample, and is only an approximation of the true p-value in general unless shown otherwise.)
There’s a small true effect, but lots of evidence. Now suppose remdesivir only reduces time to recovery by 2 days on average. We enroll 16 patients, and estimate this unknown true effect as a reduction of 2.2 days, with a “very significant p-value” of 0.0002. (Our much larger sample size here has gotten us a much more precise estimate of the true effect.) The effect is small enough that we needed 16 patients to see it.
Most would agree that the first finding is more intuitively “significant”: Bigger is better. However, both findings are “statistically significant”, with the 10.6-day estimate being “less significant” (i.e., bigger p-value) than the 2.2-day estimate—counter to intuition. These two simple scenarios show why “significance”—used as the common, misguided shorthand for the entire phrase “statistical significance”—does not imply scientific or clinical “importance”.
The simple fix: Never just say “significant” when you really mean “statistically significant”. You will be misunderstood as saying “important”. Instead, always say or write out the whole phrase “statistically significant”.
(For a deeper dive into this example, see the Appendix for R code and the full simulation results.)
Not Just Academic
Of course, a statistically significant finding like the one in the news still conveys good news: In this RCT, there seems to be enough statistical evidence for a clinically meaningful reduction in time-to-recovery from 15 days to 11 when taking remdesivir (provided the RCT was powered appropriately; see Brownlee, 2018 for a Python statistical power tutorial). That is, there may have been enough statistical support (i.e., from a sample of 1,063 patients) to claim this effect size might be close to what’s real.
But what if scenario 2 above had been the case? The media or health experts would have reported that “remdesivir significantly reduced time-to-recovery from 15 days to 13” (rounded). Come again?
Never just say “significant” when you really mean “statistically significant”. You will be misunderstood as saying “important”. Instead, always say or write out the whole phrase “statistically significant”.
Think about what this means clinically. A 2.2-day reduction is likely not as clinically important as a 10.6-day reduction. But the media and health experts would have called both reduction estimates “significant”, mistakenly thinking they were reporting clinical importance. That is, they would have confused a statistical finding with a scientific or clinical one.
Importantly, note that even medical doctors and health experts make this mistake. All. The. Time.
That means this distinction between “statistical significance” and “clinical importance” is not just academic. It has real-world public health and policy implications in shaping how leaders decide what to recommend in treating COVID-19 patients.
Statistics helps science—but is not, itself, science.
But why do even experts make this mistake? I believe the reason is related to the popularity of the phrase “correlation does not imply causation”: We can all say it—but we all still constantly struggle to follow it. My understanding and opinion is that evolution has hardwired us to mistake correlation for causation: Seeing causes and effects—even when there were none—was more important in keeping us alive in ages past than occasionally committing this cognitive error. My guess is that we’re predisposed to be results-oriented rather than evidence-oriented for reasons similar to why we’re predisposed to be causality-oriented rather than association-oriented. (Evolutionary psychologists and cognitive scientists, your thoughts?)
But in today’s world, committing the significance fallacy has society-wide consequences—not just personal or tribal ones. Influential leaders enacting policies that affect hundreds, thousands, and millions of people cannot afford to make this mistake. It takes concerted mental vigilance not to succumb to natural intuition. Even we statisticians, who are specifically trained how not to make this mistake, still slip up: We’re human, after all. (No, really!)
Summary
Statistics helps science—but is not, itself, science. Whenever you call a “statistically significant” finding simply “significant”, you erroneously conflate statistics with science (Wasserstein and Lazar, 2016). It’s only natural, from what I can tell.
Far from being pedantic and academic, the significance fallacy has serious health implications: Unwittingly confusing statistics with science (particularly for small effect sizes) shapes policies and medical practices affecting millions of people. This impacts your health every day—and that of your friends and family.
But as we saw, there’s hope. We can all learn to do the following:
- Ask yourself if an RCT’s reported effect size estimate is meaningful, regardless of sample size.
- Train yourself to internalize that significance does not imply importance.
- Remember that sample size does not correlate with effect size.
- Never just say “significant” when you really mean “statistically significant”. You will be misunderstood as saying “important”. Instead, always say or write out the whole phrase “statistically significant”.
If enough of us can do these four things, we can help our leaders do likewise—or become significant leaders, ourselves.
References
Barnett ML, Mathisen A. Tyranny of the p-value: the conflict between statistical significance and common sense. 1997: 534–536. journals.sagepub.com/doi/pdf/10.1177/00220345970760010201
Brownlee J. A Gentle Introduction to Statistical Power and Power Analysis in Python. Statistics. 2018 Jul 13. machinelearningmastery.com/statistical-power-and-power-analysis-in-python/
Kühberger A, Fritz A, Lermer E, Scherndl T. The significance fallacy in inferential statistics. BMC research notes. 2015 Dec;8(1):84. bmcresnotes.biomedcentral.com/track/pdf/10.1186/s13104-015-1020-4
Silva-Ayçaguer LC, Suárez-Gil P, Fernández-Somoano A. The null hypothesis significance test in health sciences research (1995–2006): statistical analysis and interpretation. BMC medical research methodology. 2010 Dec 1;10(1):44. link.springer.com/article/10.1186/1471-2288-10-44
Sullivan GM, Feinn R. Using effect size—or why the P value is not enough. Journal of graduate medical education. 2012 Sep;4(3):279–82. www.jgme.org/doi/full/10.4300/JGME-D-12-00156.1
Wasserstein RL, Lazar NA. The ASA statement on p-values: context, process, and purpose. 2016. tandfonline.com/doi/full/10.1080/00031305.2016.1154108
Appendix
Proof Sketch: Significance Does Not Imply Importance
P-value Definition
In Chapter 10.3 “Common Large-Sample Tests” of Wackerly et al (2014), for a continuous random variable \(Y\), estimating the population mean \(E(Y)\) is usually of interest. Under the null hypothesis, \(H_0: E(Y) = \mu_0\) for some null population mean \(\mu_0\) (e.g., \(\mu_0 = 0\)). The common two-sided alternative hypothesis is \(H_a: E(Y) < \mu_0 \text{ or } E(Y) > \mu_0\), or simply \(H_a: E(Y) \ne \mu_0\).
These null and alternative hypotheses can be written in terms of the true effect size \(\delta = E(Y) - \mu_0\) as \(H_0: \delta = 0\) and \(H_a: \delta \ne 0\). Note that the sample size \(n\) is not mathematically related to the true effect size: There is no “\(n\)” in the expression “\(E(Y) - \mu_0\)”. Loosley speaking, “sample size does not correlate with effect size”.
Let’s use \(\bar{Y}_n = (1/n) \sum_{i=1}^n Y_i\), an unbiased estimator of \(E(Y)\), with variance \(V \left( \bar{Y}_n \right) = \sigma^2 / n\) (i.e., standard error \(\sigma / \sqrt{n}\)) where \(\sigma^2 = V(Y)\) is the variance of \(Y\) (i.e., standard deviation \(\sigma\)). Let \(\Delta_n = \bar{Y}_n - \mu_0\) denote the random sample effect size estimate. The common test statistic for these hypotheses is:
\[ Z_n = \frac{\Delta_n}{\sqrt{\sigma^2 / n}} \] By the central limit theorem, \(Z_n\) is approximately distributed as the standard normal random variable \(Z \sim N(0, 1)\) if \(H_0\) is true, with this approximation improving as \(n\) gets large. That is, \(Z_n\) converges in distribution to \(Z\) as \(n\) approaches infinity; see Theorem 7.4 in Wackerly et al (2014). Recall that this is true even if \(Y\) is not normally distributed because \(Z_n\) is a distribution of the sample mean of \(Y\) (i.e., \(\bar{Y}_n\))—not of \(Y\) itself.
Hence, the usual p-value for the test statistic \(z_n\) corresponding to a given sample \(\{ y_1, \dots, y_n \}\) when looking for evidence in favor of this two-sided \(H_a\) is:
\[ p(z_n) = P ( Z \le - \big| z_n \big| ) + P ( Z \ge \big| z_n \big| ) = 2 P \left( Z \ge \frac{ \big| \delta_n \big| }{\sqrt{\sigma^2 / n}} \right) \]
To see that this makes sense, consider the usual approach of setting an arbitrary “statistical significance level” cutoff \(\alpha\) (e.g., 0.05) such that the sample effect size \(\delta_n\) is said to be “statistically significant” if \(p(z_n) < \alpha\). For our two-sided test, \(\delta_n\) is said to be “statistically significant” if \(P \left( Z \ge \big| \delta_n \big| \big/ ( \sqrt{\sigma^2 / n ) } \right) < \alpha / 2\).
Proof Sketch
Statistically Equivalent Sample Effect Sizes
Let \(\bar{Y}_{nj} = (1 / n_j) \sum_{i=1}^{n_j} Y_{ij}\) represent the average outcome for sample \(j\), and let \(\Delta_{nj} = \bar{Y}_{nj} - \mu_0\) and \(Z_{nj} = \Delta_{nj} \big/ \sqrt{\sigma^2 / n_j}\). Any pair of test statistics \(\{ z_{n1}, z_{n2} \}\) are equal if and only if:
\[ z_{n1} = \frac{\delta_{n1}}{\sqrt{\sigma^2 / n_1}} = \frac{\delta_{n2}}{\sqrt{\sigma^2 / n_2}} = z_{n2} \] \[ \delta_{n1} \sqrt{n_1} = \delta_{n2} \sqrt{n_2} \] \[ \delta_{n1} \sqrt{\frac{n_1}{n_2}} = \delta_{n2} \]
So the p-value for sample effect size \(\delta_{n1}\) is identical to the p-value for another sample effect size \(\delta_{n2}\) if \(\delta_{n2} = \delta_{n1} \sqrt{n_1 / n_2}\).
Proof by Contradiction
Consider positive sample effect sizes. Suppose we say that \(\delta_{n1}\) is more “important” than \(\delta_{n2}\) if \(\delta_{n1} > \delta_{n2}\); i.e., intuitively, bigger is better. We can say that statistical significance implies importance if \(p(z_{n1}) < p(z_{n2})\) implies \(\delta_{n1} > \delta_{n2}\) for any \(\{ \delta_{n1}, \delta_{n2} \}\). That is, the p-value for any less-important sample effect size \(\delta_{n2}\) is always larger than that of \(\delta_{n1}\). We will prove that statistical significance does not imply importance by these definitions.
Proof
- Suppose statistical significance implies importance as defined above.
- Choose \(\delta_{n2}\) such that \(\delta_{n1} < \delta_{n2}\). That is, \(\delta_{n2}\) is more important than \(\delta_{n1}\).
- Choose \(n_k < n_1\) such that \(\delta_{n1} \sqrt{n_1 / n_k} > \delta_{n2}\).
- Then \(z_{n1} > z_{n2}\) and \(p(z_{n1}) < p(z_{n2})\), a contradiction. That is, \(\delta_{n1}\) is less important than \(\delta_{n2}\) but implies \(p(z_{n1})\) is more statistically significant than \(p(z_{n2})\).
Figures 1 and 2 illustrate one such example of this contradiction. There, we see that a big estimated reduction of \(\delta_{n2} =\) 12 days to recovery from a hypothetical study enrolling \(n_2 =\) 3 patients is less statistically significant with \(p(z_{n2}) =\) 0.0091 than a small estimated reduction of \(\delta_{n1} =\) 2 days with \(p(z_{n1}) =\) 0.0012 from a study enrolling \(n_1 =\) 16 patients.
Loosely speaking, it is mathematically impossible to tell if a finding is clinically or scientifically important just from knowing whether or not it was “statistically significant”. Succinctly, statistical significance does not imply importance (as intuitively defined here).
References
- Wackerly D, Mendenhall W, Scheaffer RL. Mathematical statistics with applications. Cengage Learning; 2014 Oct 27. cengage.com/c/mathematical-statistics-with-applications-7e-wackerly/9780495110811/
RCT Simulations
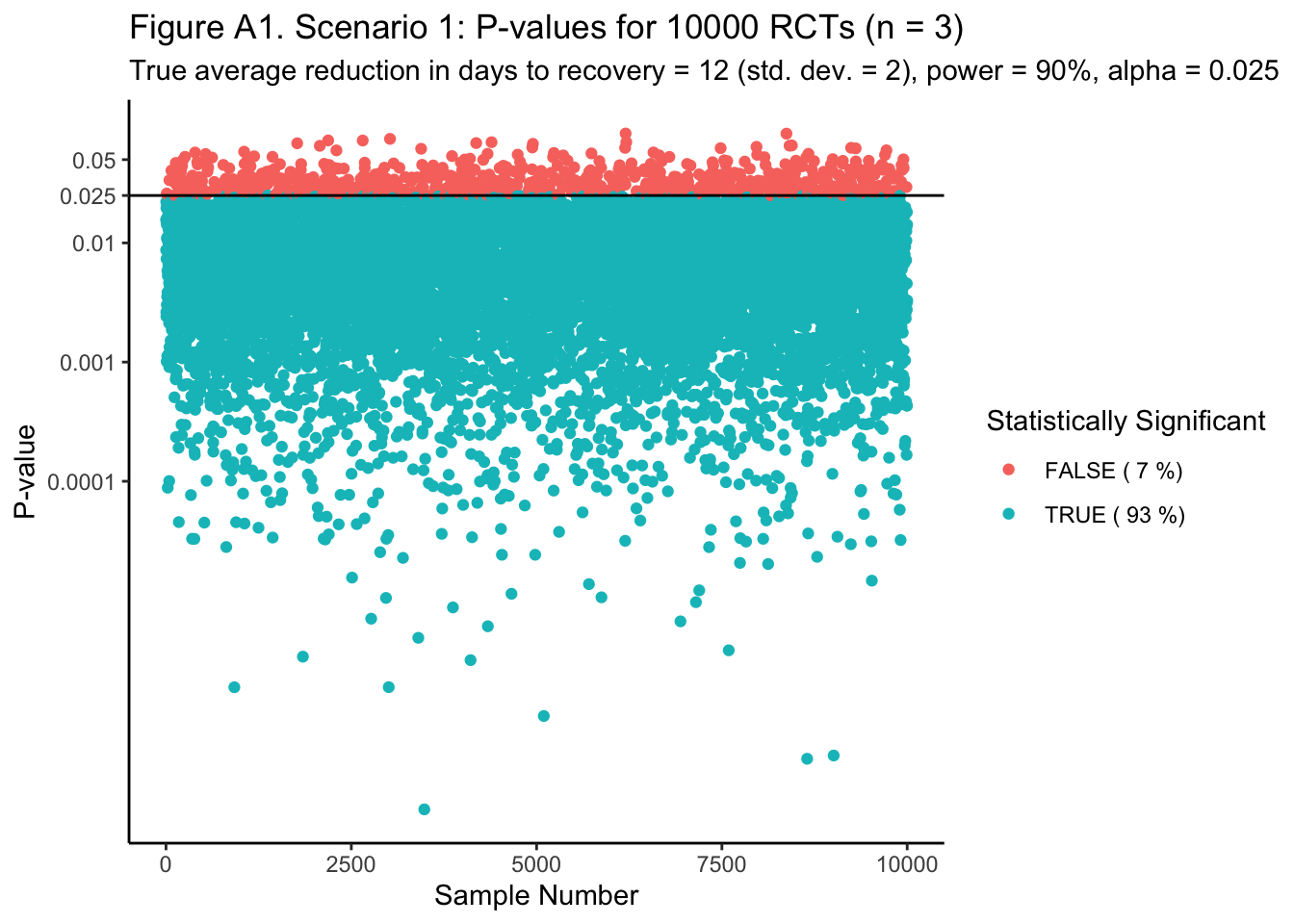
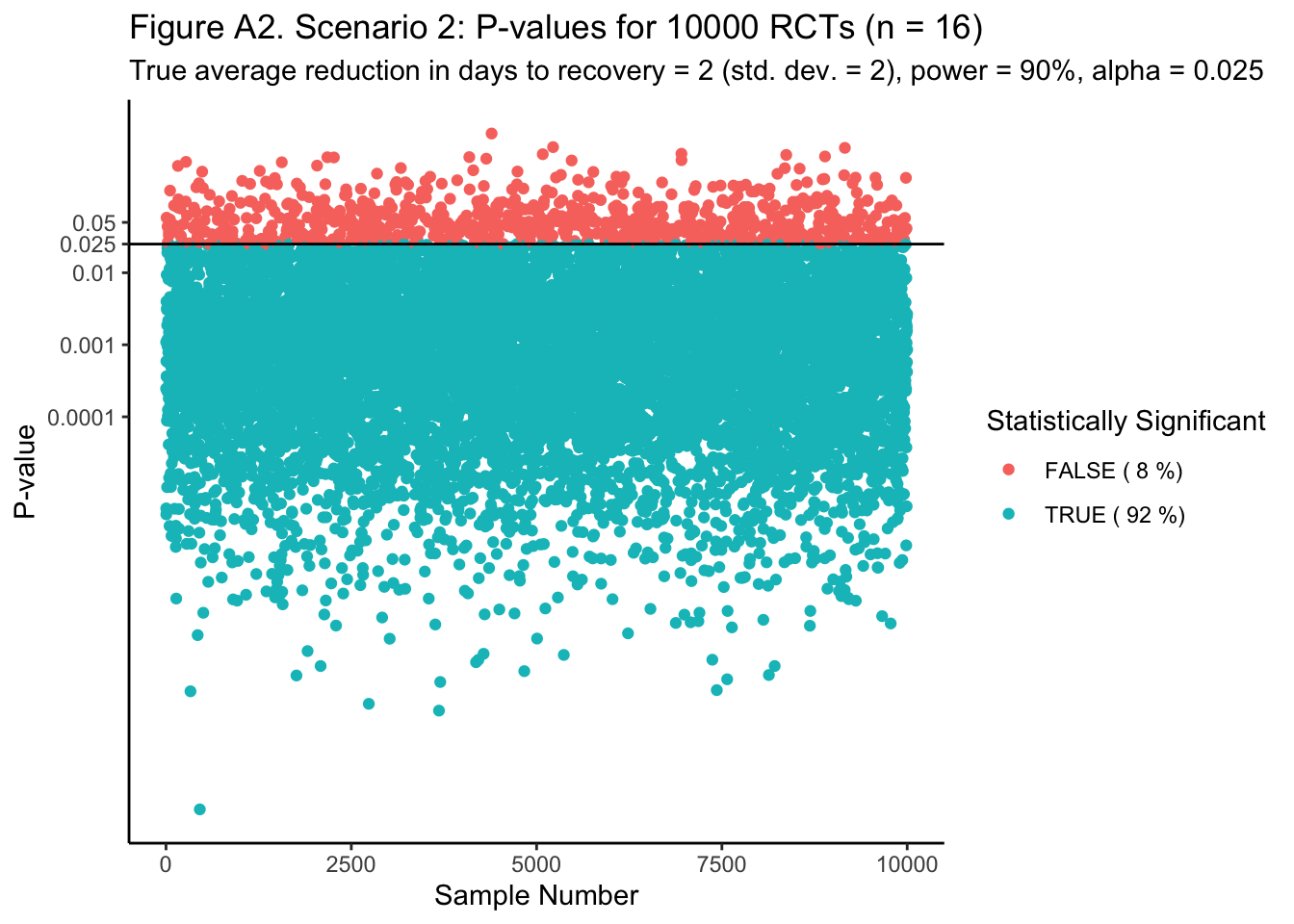
In Figure A1 (ggp_pvalues1 below), we see that 93% of all 10,000 simulated RCTs gave us statistically significant estimates of a true difference of 12 (at the 0.025 overall level of statistical significance). In Figure A2 (ggp_pvalues2 below), we see that 92% of all RCTs likewise gave us statistically significant estimates of a true difference of 2.
